R^2 ("R squared") envy
Was at a conference recently & a (perfectly nice & really smart) guy in the audience warns everyone not to take social psychology data on risk perception too seriously: "some of the studies have R2's of only 0.15...."
Oy.... Where to start? Well how about with this: the R2 for viagra effectiveness versus placebo ... 0.14!
R2 is the "percentage of the variance explained" by a statistical model. I'm sure this guy at the conference knew what he was talking about, but arguments about whether a study's R2 is "big enough" are an annoying, and annoyingly common, distraction.
Remarkably, the mistake -- the conceptual misundersandings, really -- associated with R2 fixation were articulated very clearly and authoritatively decadesago, by scholars who were then or who have become since giants in the field of empirical methods:
- Abelson, R.P. A Variance Explanation Paradox: When a Little is a Lot. Psychological Bulletin 97, 129-133 (1985).
- King, G. How Not to Lie with Statistics. Am. J. Pol. Sci. 30, 666-687 (1986).
- Rosenthal, R. & Rubin, D.B. A Note on Percent Variance Explained as A Measure of the Importance of Effects. J. Applied Social Psychol. 9, 395-396 (1979).
I'll summarize the nub of the mistake asssociated with R2 fixation but it is worth noting that the durability of it suggests more than a lack of information is at work; there's some sort of congeniality between R2 fixation and a way of seeing the world or doing research or defending turf or dealing with anxiety/inferiority complexs or something... Be interesting for someone to figure out what's going on.
But anyway, two points:
1. R2 is an effect size measure, not a grade on an exam with a top score of 100%. We see a world that is filled with seeming randomness. Any time you make it less random -- make part of it explainable to some appreciable extent by identifying some systematic process inside it -- good! R2 is one way of characterizing how big a chunk of randomness you have vanquished (or have if your model is otherwise valid, something that the size of R2 has nothing to do with). But the difference between it & 1.0 is neither here nor there-- or in any case, it has nothing to do with whether you in fact know something or how important what you know is.
2. The "how important what you know is" question is related to R2 but the relationship is not revealed by subtracting R2 from 1.0. Indeed, there is no abstract formula for figuring out "how big" R2 has to be before the effect it mesaures is important. Has extracting that much order from randomness done anything to help you with the goal that motivated you to collect data in the first place? The answer to that question is always contextual. But in many contexts, "a little is a lot," as Abelson says. Hey: if you can remove 14% of the variance in sexual performance/enjoyment of men by giving them viagra, that is a very practical effect! Got a headache? Take some ibuprofen ( R2 = 0.02).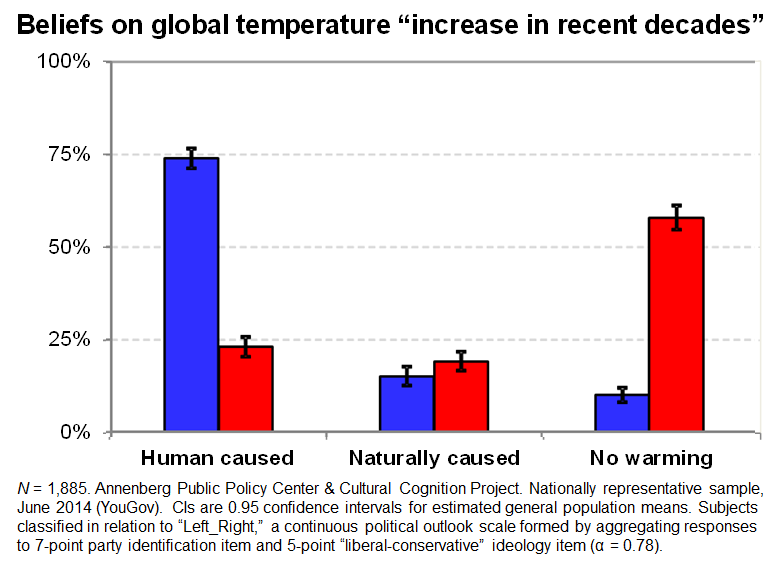
What about in a social psychology study? Well, in an experimental study, that I and some others conducted of how cultural cognition shaped perceptions of the behavior of political protesters, the R2 for the statistical analysis was 0.19. To see the practical importance of an effect size that big in this context, one can compare the percentage of subjects identified by one or another set of cultural values who saw "shoving," "blocking," etc., across the experimental conditions.
If, say, 75% of egalitarian individualists in the abortion-clinic condition but only 33% of them in the military-recruitment center condition thought the protestors were physically intimidating pedestrians; and if only 25% of hierarchical communitarians in the abortion-clinic but 60% of them in the recruitment-center condition saw a protestor "screaming in the face" of a pedestrian--is my 0.19 R2 big enough to matter? I think so; how about you?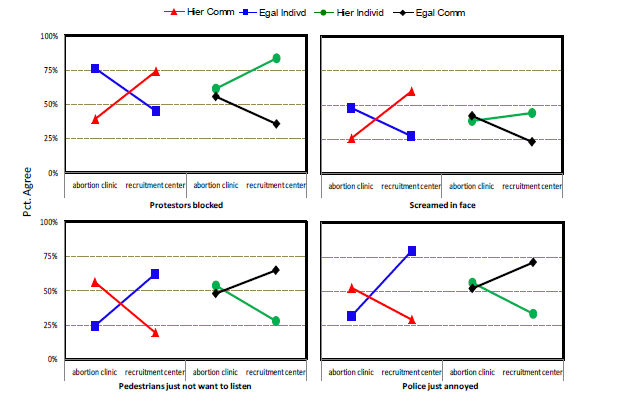
There are cases, too, where a "lot" is pretty useless -- indeed, models that have notably high R2's are often filled with predictors the effects of which are completely untheorized and that add nothing to our knowledge of how the world works or of how to make it work better.
Bottom line: It's not how big your R2 is; it's what you (and others) can do with it that counts!
cross posted from http://www.culturalcognition.net/blog/
